Create a repository at GitHub
Firstly, we need a remote repository to start. I will use GitHub to host our remote repository. Sign up from here to get an account at GitHub. After sign in, click the  icon and select New repository.
icon and select New repository.
 icon and select New repository.
icon and select New repository.
In the next screen, give a name "HelloWorld" to our repository. You can also write a brief description about the repository, so other people will know what is your repository about. Choose Public as the repository type, so it can be accessed by anyone with restriction on modification. Private repository is available to paid users. If you tick Initialize this repository with a README, GitHub will create a read me file in the repository. We leave it as it is so we will have a clean repository. Then click the Create repository button and our HelloWorld repository is created.
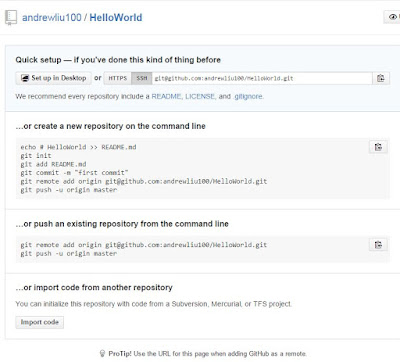
In the next screen, you can see the HelloWorld repository is empty and GitHub provides several suggestions to start with. We will leave it for now and go back to HelloWold project in Eclipse.
SSH configuration
If you are going to use SSH protocol instead of HTTP for read and write access to the remote repository at GitHub, you have to configure the SSH key in Eclipse and GitHub.
Eclipse SSH configuration
Open Eclipse Preferences via Windows -> Preferences. Then go to General -> Network Connections -> SSH2. Select Key Management tab and click the Generate RSA Key... button. Eclipse will generate a public key (Copy the public key to a text file and it will be uploaded to GitHub later). Then enter a pass phrase in Passphrase: and Confirm passphrase: fields, it will be used to protect the private key. Click the Save Private Key... button to save the private key in your computer (usually it is saved in C:\Users\<username>\.ssh). Then go to General tab and enter the path of the private key (usually is C:\Users\<username>\.ssh) in SSH2 home: field. Click Apply button to save the configuration.
GitHub SSH configuration
Log in to GitHub. Then click the  icon on the top right of the screen and select Settings in the menu. Choose SSH Keys in the navigator on the left. Then click Add SSH Key button and paste the Eclipse generated public key into the Key text box. Title field is optional.
icon on the top right of the screen and select Settings in the menu. Choose SSH Keys in the navigator on the left. Then click Add SSH Key button and paste the Eclipse generated public key into the Key text box. Title field is optional.
 icon on the top right of the screen and select Settings in the menu. Choose SSH Keys in the navigator on the left. Then click Add SSH Key button and paste the Eclipse generated public key into the Key text box. Title field is optional.
icon on the top right of the screen and select Settings in the menu. Choose SSH Keys in the navigator on the left. Then click Add SSH Key button and paste the Eclipse generated public key into the Key text box. Title field is optional.
Click Add key button and you will be asked to confirm your password. After the password is confirmed, the public key is added to GitHub. Now you are able to use SSH protocol to access your repositories at GitHub.
Push the local repository to remote repository
Firstly, we need a local repository to push. Create the HelloWorld project in Eclipse and share it in a local Git repository. Please refer to Git with Eclipse (3) - basic use cases in EGit with local repository for how to share project in local repository.
Secondly, because we created an empty repository at GitHub in previous step, we need to create a branch in the remote repository. Open Git perspective in Eclipse by selecting Windows -> Open Perspective -> Other....in the menu, then choose Git in the opened dialog.
Secondly, because we created an empty repository at GitHub in previous step, we need to create a branch in the remote repository. Open Git perspective in Eclipse by selecting Windows -> Open Perspective -> Other....in the menu, then choose Git in the opened dialog.
In the Git perspective, expand HelloWorld repository, right click on Remotes and select Create Remote... In the menu.
Give a remote name in the opened dialog (Usually is origin by default) and select Configure push, then click OK.
The Configure Push dialog asks for the URI of the remote repository. we can copy the URI from HelloWorld repository at GitHub (we will use SSH URI in our example). Log in to GitHub and open HelloWorld repository. In the top section of the page, click on SSH and click the icon to copy the SSH URI.
icon to copy the SSH URI.
 icon to copy the SSH URI.
icon to copy the SSH URI.
Then go back to Eclipse. Click the Change... button in Configure Push dialog and paste the SSH URI into the URI: field in the opened Destination Git Repository dialog. Select ssh in the Protocol: field. Authentication Users: is git. Leave the rest as what it is and click Finish. You will be asked for the pass phrase. Enter the pass phrase you have set up in the SSH configuration and click OK.
Then click Save and Push button in Configure Push dialog.
A confirmation window will be shown once the repository is pushed to GitHub successfully.
Click OK to close the window. Log in to GitHub and open HelloWorld repository. You will see the HelloWorld project is now available at GitHub.
Now the HelloWorld project is ready to be forked or collaborated by other contributors. Also, you can fetch any updates in the HelloWorld project from GitHub and push your changes in HelloWorld project to GitHub. For how to clone a remote repository and fetch/push changes. Please read Git with Eclipse (5) - work with remote repositories (coming soon...).
Reference: